Rezime

Tačno numeričko modeliranje krivolinijskih grednih nosača je od izuzetnog značaja u mnogim inženjerskim oblastima. Geometrija krivolinijskog grednog nosača, diskretizacija grede kao i potrebne pretpostavke grede, predstavljaju poteškoće prilikom formulacije krivolinijskog grednog elementa.

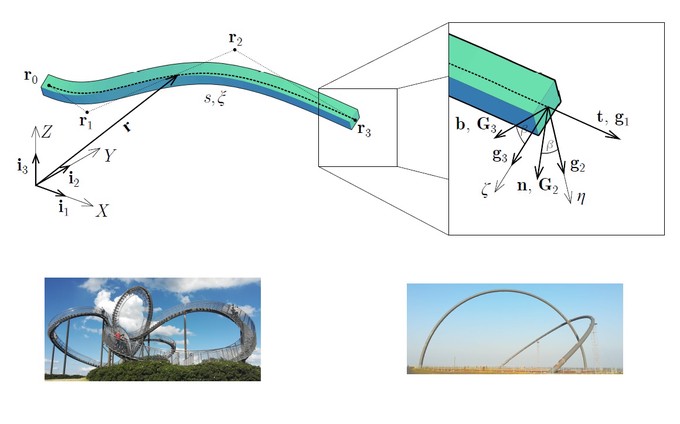
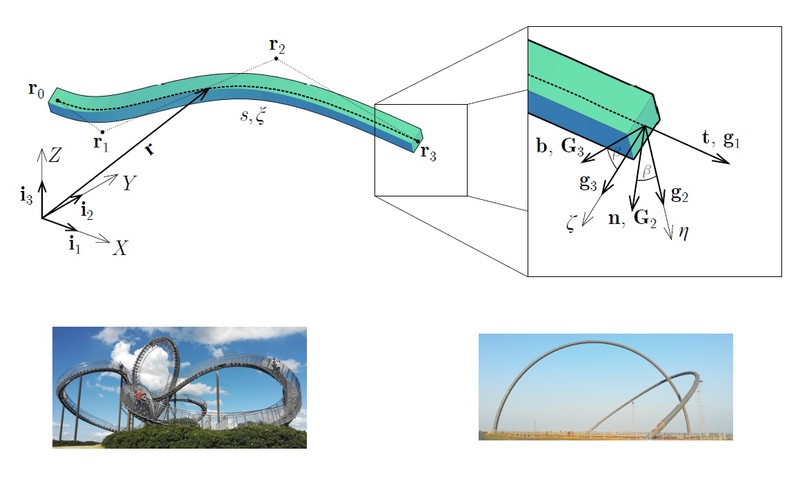
U ovom radu je primenjen izogeometrijski pristup u dinamičkoj analizi prostornih krivolinijskih grednih nosača. Novi gredni element je definisan primenom Bernuli - Ojlerove pretpostavke, kao i osnovnih relacija diferencijalne geometrije i mehanike kontinuuma Košijeve grede. Geometrija grede, kao i polje pomeranja, brzine i ubrzanja su definisani primenom NURBS baznih funkcija, što predstavlja fundamentalnu osobinu izogeometrijskog pristupa. Složena geometrija krivolinijskog grednog nosača može se tačno modelirati primenom izogeometrijskog pristupa zasnovanog na NURBS baznim funkcijama. Formulacija prostornog krivolinijskog grednog nosača je izvedena u uslovima linearne teorije, dok je geometrijski nelinearna teorija primenjena samo na ravanskom krivolinijskom grednom nosaču, primenom eksplicitne metode integracije. Izvršena je analiza slobodnih i prinudnih vibracija. Analiza prinudnih vibracija je fokusirana na uticaj pokretnog opterećenja na krivolinijski gredni nosač. Primenom date formulacije dobijeni su rezultati zadovoljavajuće tačnosti sa manje stepeni slobode u poređenju sa klasičnom metodom konačnih elemenata. U skladu sa tim, u cilju dobijanja rezultata zadovoljavajuće tačnosti krivolinijskog grednog nosača, nepohodna je primena manje resursa. Ovo čini prikazani pristup konkurentnijim klasičnoj metodi konačnih elemenata u analizi fleksibilnih inženjerskih konstrukcija sa složenom geometrijom.