Abstract

Accurate numerical modeling of curved beams is of significant importance in different engineering fields. Several challenges can be present during the curved beam formulation, primarily due to the issues regarding the beam geometry, discretization and beam theory assumptions.

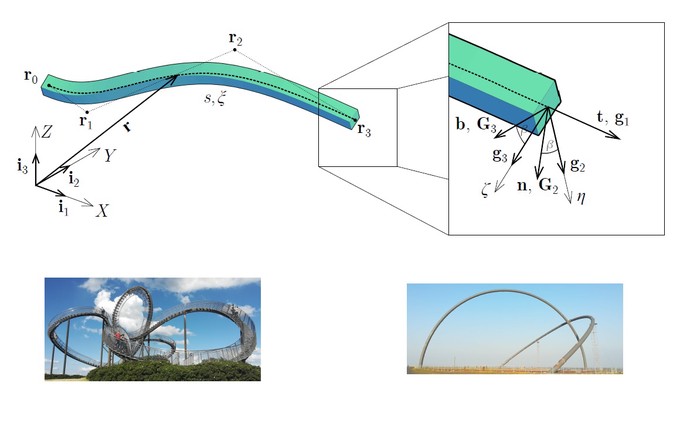
In this dissertation, the isogeometric approach is applied in the dynamic analysis of spatial curved beams. A novel beam element was formulated using the Bernoulli - Euler hypothesis and the fundamental relations of the differential geometry, as well as the Cauchy continuum beam model. The geometry of the beam, as well as the displacement, velocity and acceleration fields, were defined using the Non-Uniform Rational B-Spline (NURBS) basis functions, which present the basis concept of the isogeometric approach. Complex geometry of the curved beams can be modeled accurately using NURBS - based isogeometric approach. Formulation of the spatial beam is conducted for the linear case, while the geometrically nonlinear formulation is conducted only for the plane curved beam using an explicit integration procedure. Free and forced vibration analyses of the curved beams are studied. In the latter, the influence of the moving mass on the curved beams is analyzed. The presented approach had shown that, in comparison to the classical finite element method (FEM), a less number of degrees of freedom are required in order to obtain accurate results. Consequently, fewer computational resources are needed to reach the appropriate level of accuracy for the curved beams. This makes the presented approach competitive with the conventional FEM, especially in the analysis of the flexible spatial engineering structures with complex geometry.