Abstract

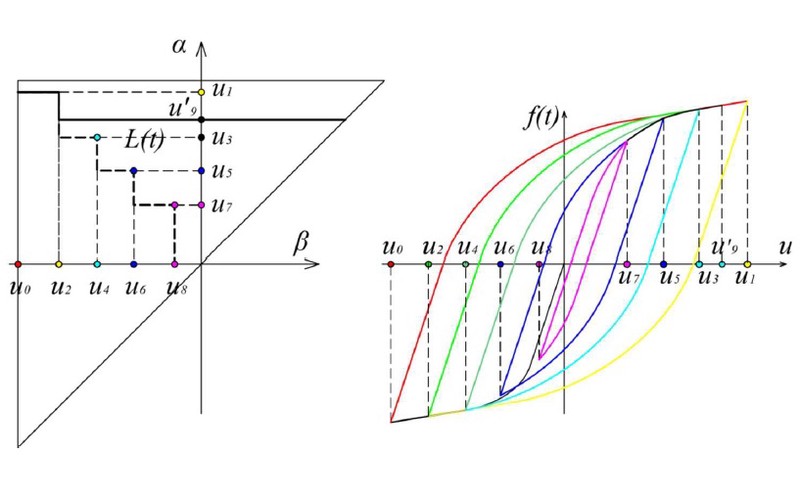
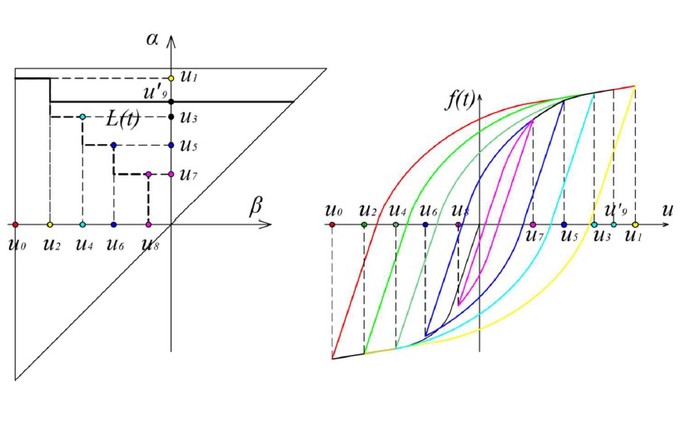
In this doctoral dissertation, the elastoplastic behavior of structural mild steel under large deformations is explained. It will be shown that the stress-strain diagram's main characteristic of this steel type is the formation of a horizontal yield plateau between the elastic region and the plastic hardening region. This phenomenon, manifested in the form of local instability of the atomic lattice (Luders band), is only a characteristic of monotonic loading, whereas in the case of alternating loading it disappears. Using Preisach's hysteresis operator, a material model was developed, describing with excellent accuracy the behavior of this type of steel under monotonic axial loading. The material model in the form of an analytical expression for the strain-stress relationship very well approximates the regions of elasticity, horizontal yield plateau, and plastic hardening characterized for structural mild steel under this type of loading. Based on this initial model, the new model of hysteresis, fully defining the cyclic behavior of structural mild steel, was developed. Firstly the trend line composed from peaks of closed hysteresis loops with maximum amplitudes up to the observed time t (backbone curve) is defined and then also the formation of internal hysteresis loops, which takes into account the effects of cyclic hardening. These phenomena will be taken into account through changes in the values of the basic material characteristics (corresponding modulus of elasticity and yield limits). The material model formed on this way, is phenomenologically much better suited for the description of the real material behavior, than all existing hysteresis models. The finite element method equations for elastoplastic analysis of girders whose elements are axially loaded (eg trusses) are defined based on this model. In this dissertation, the existing models defining the elastoplastic behavior of structural mild steel have been upgraded to describe the damage effects in the material through two different approaches. In the first Preisach model, the stiffness drop inside the damage zone is modeled by an elastic element of negative stiffness implemented into a mechanical model. For the second approach, the mechanical model was modified using an element with a defined limit of damage initiation. Both models are suitable for describing damage at both monotonic and cyclic stresses. In models that define the cyclic behavior of this steel type, the damage causes a drop within the stress-strain backbone curve. This stress drop, with a reduction of the surfaces of the internal hysteresis loops, also models the effect of cyclic softening for stresses beyond the initiation damage limit. The energy dissipation during the formation of hysteresis loops due to cyclic stress is manifested through hysteresis losses. The incremental procedure based on which it is possible to define the realized plastic work, energy losses, and captured energy, was defined based on the suggested hysteresis model. Procedures can be defined for models with and without damages both, using the appropriate Preisach function. The basis for extending the analysis to beam elements is given through a geometric interpretation of the problem in the form of a Preisach prism. For rectangular cross-sections, exposed to pure bending, the possibility of moments calculation is presented, based on the assumption of engineering beam theory (cross-section is perpendicular to a bending line). The basis of the calculation is the numerical integration of the deformations along with the height of the cross-section. The observed hysteresis models were derived by looking at the case of large straining in plastic region, without considering the effect of fatigue on the appearance and propagation of the damage in the material. In this dissertation, based on the nonlocal memory property of the Preisach models, a new method for determining the number of full cycles for an arbitrary load history (staircase method) is determined. The implementation of this method, with the elimination of the existing cycle counting methods shortcomings, enables the implementation of the fatigue effect in the analysis of structures under load with arbitrary load history. Also, simplifying the calculation of energy losses by identifying and pairing hysteresis loops with the equivalent surfaces is provided. To validate the results and determine material characteristics of the model used in this dissertation, the results obtained by the analyzed Preisach model were compared with experimental results. The experiments were conducted on cylindrical specimens made of structural mild steel with a pronounced yield plateau under monotonic and cyclic stress regimes.