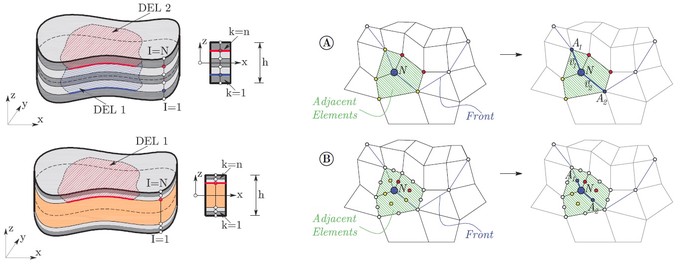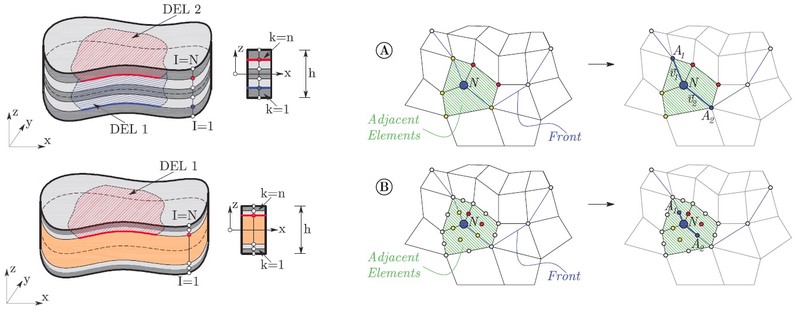
Nonlinear analysis of laminated composite plates and shells with delaminations using finite element method
Abstract
Laminated composites play an important role in the construction of aircrafts, wind turbines, ships, cars and other components in mechanical and civil engineering. For example, the aerospace structures are made of thin-walled cylindrical or spherical composite shell components having an excellent stiffness-to-weight and strength-to-weight ratios. It is also well-known that Fiber Reinforced Polymer strengthening of the RC beams and slabs give excellent structural results, low time required and moderate cost. Finally, sandwich plates are widely used in civil engineering as roof and wall panels to provide the thermal isolation of the buildings. For these reasons, numerical analysis of laminated composite and sandwich structures attract the increasing attention of researchers in the various engineering disciplines. It is very important that perfect bond between the adjacent layers within the laminate remain intact for the panel to perform on the designed level. However, the mismatch of material properties between the adjacent layers, along with some other factors, may cause a delamination that reduces the stiffness of the component and leads to the unexpected structural behavior. To predict the response of damaged structure, a computational model capable to describe the kinematics of the delaminated structures is required. Several limitations of the Equivalent Single Layer (ESL) laminate theories motivated the researchers to derive the refined (layerwise) plate theories for the analysis of composite laminates. Therefore, the scope of this study is based on the reduction of the 3D elasticity problem to a 2D one using the Generalized Laminated Plate Theory (GLPT) of Reddy, capable to describe the delamination kinematics. The GLPT became the basis for the development of enriched layered finite elements, which are applied in the numerical solution of several structural problems. In addition, layered plate finite elements were applied in the numerical investigation of delaminated composite shells using the simple transformations presented in this study. To accurately capture the buckling phenomena of the laminated composites, as well as for investigation of the influence of large rotations on the transient response of delaminated composite and sandwich plates, the geometric nonlinearity is taken into account upon the von Karman assumptions. Beside the numerical solution, the analytical (Navier) solution for linear transient analysis of intact rectangular simply supported composite plates is provided based on double Fourier series. During the motion of the plate a small gap maybe formed between the adjacent layers in delaminated zones. Because the initially present embedded delamination can open and close in the dynamic loading environment, the node-to-node nonlinear frictionless contact algorithm which prevents the layer overlapping is introduced. In addition, energy criterion based on the Virtual Crack Closing Technique is applied in order to predict a delamination growth in static and dynamic loading environments. The algorithm allows for the change of the previously imposed delaminated zone. Finally, the differences between the solutions considering only the stationary delamination and these allowing for delamination propagation have been highlighted. Pre- and post-processing phases of the simulations are performed using the GiD Pre/Post Processor software developed in CIMNE, Barcelona. All numerical models and solution procedures are coded in original object-oriented MATLAB solver. Theoretical considerations are validated in the variety of numerical examples for bending, free vibration, buckling and transient analysis of delaminated composite and sandwich plates and shells. Whenever possible, the obtained results are compared with the exact, analytical, numerical and experimental data from the literature. In addition, the variety of new results (especially for the damaged structures) is given as the benchmark for future investigations. Finally, conclusions and the recommendations for the future work in this field are proposed.