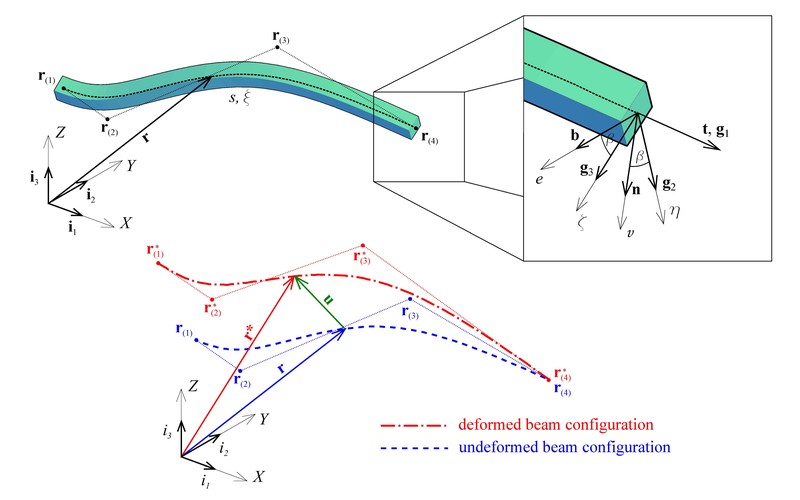
Spatial beam elements represent one of the commonly used structural elements in engineering. Due to the functional and aesthetic requirements during the design and life of the structure, demand for the spatial curved beam elements cannot be avoided. Various beam theories are used to describe the behavior of beams subjected to external loads. One of the most commonly used theory is Timoshenko beam theory where the effects of both flexural and shear deformation are considered. However, for slender beams shear locking effect can be detected. In such cases beams based on the Bernoulli–Euler hypotheses should be used. Bernoulli–Euler theory takes into account the effects of axial and flexural deformation, while the shear deformation is neglected. Calculations of the spatial beams in practical applications and software are carried out using the finite element method (FEM). One of the drawbacks of the FEM can be found in the gap between design and analysis process. Design process is performed using computer-aided design (CAD) software where the geometry is described using Non Uniform Rational B-Spline (NURBS) functions. These functions are commonly used for their capability to describe exactly the geometry of conic sections like parabola, hyperbola and elliptic configurations.

One of the initial steps in the FE analysis is mesh generation where the structure is subdivided into smaller domains called finite elements. If the refinement of the domain is required, the refined mesh has to be obtained from CAD software which affects the time necessary for the analysis. In order to overcome this gap, isogeometric approach (IGA) has been introduced. In this approach the displacement field has been described using the same functions as the geometry of structure. In the IGA, refinement procedure in the classical sense is avoided, and the refinement is conducted in the parametric domain, instead in the physical where the geometry is presented. Due to the formulation of the displacement field in the IGA, the degrees of freedom (DOF) of spatial elements based on Bernoulli–Euler hypotheses are translations and torsional rotation only. Rotations about principle axes are not taken as DOF, as in the classical FEM. Advantages of this formulation can be found in the DOF reduction in comparison to the classical formulation of the Bernoulli–Euler. It was found that the elements formulated using isogeometric approach have capability to provide accurate results. Focus of the research group is the development of isogeometric spatial beam elements based on different beam theories, for the free vibration and explicit nonlinear response analysis. Special focus is on the dynamic response of the spatial curved beam elements subjected to moving load. Based on the theoretical considerations, the original software in Matlab has been developed.