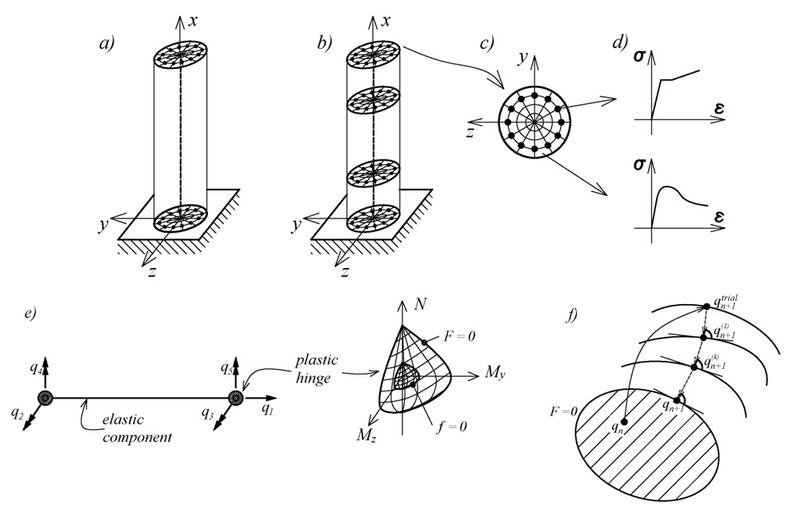
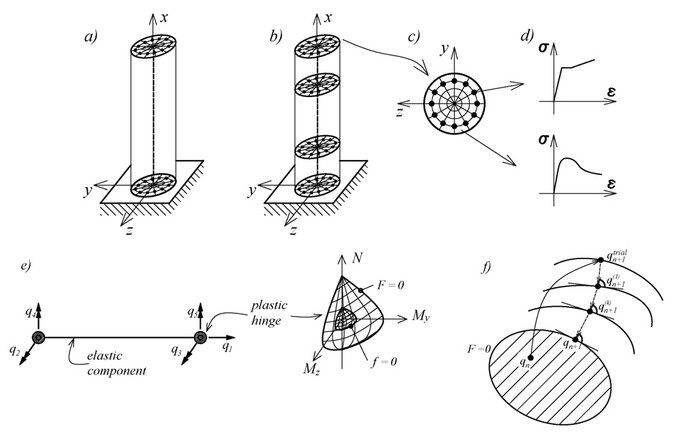
The adoption of performance-based guidelines for the earthquake resistant design of structures encourages the use of nonlinear analysis methods in professional engineering practice since they provide more detailed information about the structural response than traditional design procedures. Besides the need for more accurate computational models, it is equally important to assess the efficiency and cost of the analysis, which directly, depend on the efficiency and cost of the deployed nonlinear elements. Because of the good compromise between accuracy and computational efficiency, frame elements are commonly used in earthquake engineering practice. In this context distributed inelasticity beam-column elements with the integration of the inelastic material response over the cross-section, commonly called fiber beam-column elements, offer a high level of accuracy and flexibility in modeling the 3D inelastic response of structural members. Concentrated plasticity (point hinge) models are more economical and widely used for the simulation of the hysteretic response of frames.
Work within this topic is, on one side, focused on the development of new, advanced, 3D frame elements that take into account material nonlinearities, geometrical nonlinearities, effects of distributed plasticity and others. One newly developed element is the GP element (https://link.springer.com/chapter/10.1007/978-94-007-6573-3_3). This beam-column element with section resultant plasticity offers a good compromise between accuracy and computational cost and possess significant capabilities for the description of the global and local response of frames under monotonic and cyclic loading conditions. In the proposed element, the concept of the generalized plasticity is extended to section resultants and element deformations and is used to describe the hysteretic behavior of the plastic hinges forming at the element ends.
On the other side, the existing frame elements are improved by implementing different numerical algorithms for specific tasks within the state determination process. In fiber beam-column elements, each monitored section is discretized into fibers (or material integration points) which affords the possibility of describing the complex response of structural member. This approach also allows for consideration of residual stresses in steel members, and gradual yielding or cracking of structural members. The computational cost of the fiber beam-column element is directly dependent on the number of fibers in each monitored section. For these reasons, the development of optimal section integration scheme is of high importance. Besides, the “advanced” discretization schemes are developed that activate only when needed, which keeps the same accuracy of the fiber beam-column element but decrease computational time (costs) several times.