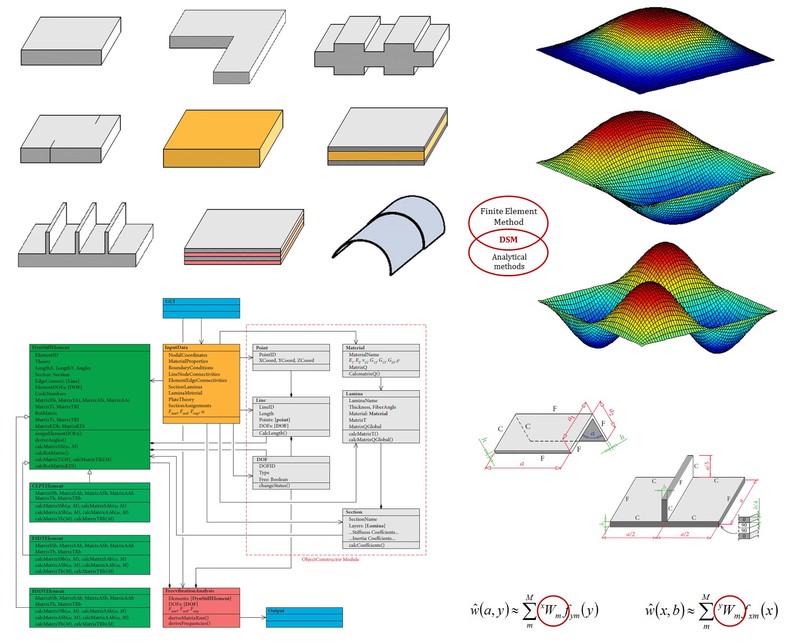
Engineering structures are usually designed to experience low frequency excitations such as wind and earthquake. However, there is a growing need for reliable prediction of the dynamic response of structures due to high frequency excitation, such as acoustics, blasts and impacts. Therefore, it is important to apply an accurate and efficient method for dynamic response analysis of such structures.
Finite element method (FEM) is most frequently used method for structural modeling. However, in mid and high-frequency ranges, the computation of the free vibration response using conventional FEM requires very fine mesh of finite elements, leading to the large number of governing equations to be solved and increasing the computational cost. Consequently, the results may become inaccurate and unreliable. To overcome these issues, the dynamic stiffness method (DSM) is applied to analyze a wide range of vibration problems.
The core of the DSM is the frequency domain-based strong-form solution of the governing equations of motion derived for the corresponding elastodynamic problem. Therefore, the number of dynamic stiffness elements necessary for structural discretization is frequency independent and influenced only by the change in the geometrical and/or material properties of the structure. At the same time, using simple assembly procedure as in the FEM makes the DSM an
efficient and highly accurate method capable of solving a broad variety of vibration problems.

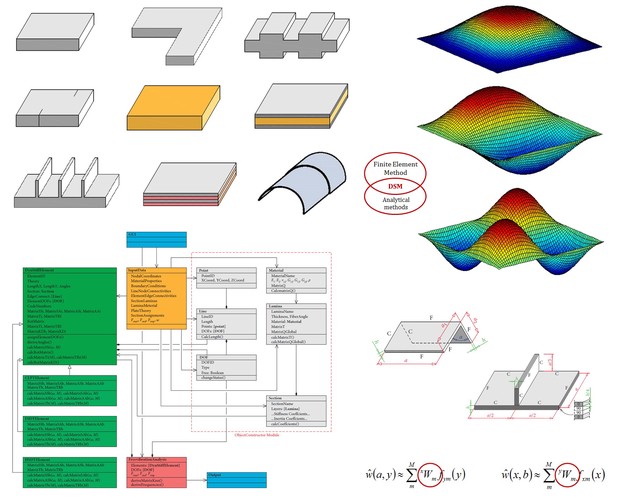
Mode shapes of stiffened plate and circular cylindrical shell using DSM
Main activities of the research group on "Dynamic Stiffness Method" are directed toward the development of dynamic stiffness elements of plates and shells and their application in the vibration of single-layer or multi-layer structures considering different material properties (isotropic or orthotropic) as well as plate and shell theories.
Based on the formulated dynamic stiffness elements, FREEVIB object-oriented software in Python environment has been created. It enables free vibration study of plate-like structures including stepped, stiffened and folded plate structures, implying isotropic or orthotropic material formulations and arbitrary boundary conditions.