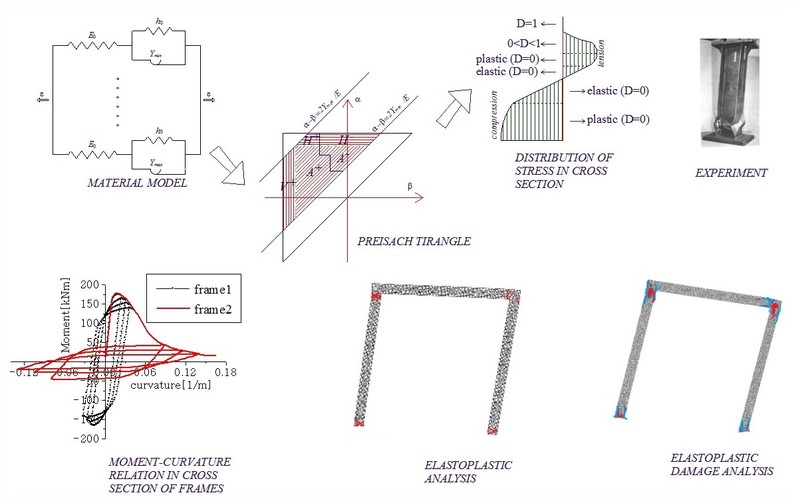
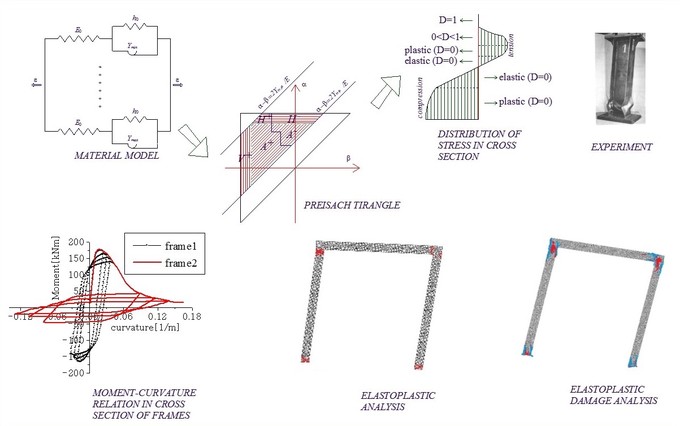
Basic principles and methodology of damage mechanics are being used in contemporary engineering problems in industry and civil engineering. In the case of material nonlinearity of cyclically loaded frame elements, numerical analysis can be a very demanding task, hence the aim of this research is to optimize structural analysis with the respect to the computational efficiency and accuracy. One of the practical methods for this type of problems is the application of hysteretic operator (Preisach model) that can reproduce very efficiently input-output relation as an analytical solution in closed form. The basis of the effective implementation of the Preisach model lies in the geometrical interpretation that is absolutely equivalent to the analytical model. Based on of the geometrical definition, it is possible to design the numerical model that enables achieving convergence at only one increment per load step, which contributes to the overall numerical performance at the structural level. It can be said that the resulting material behavior and assumption used in the formulation of the proposed analysis is suitable for describing of phenomena of ductile metals. However, the basic principles are applicable to other types of material as well. Material nonlinearity considers both plastic deformation and damage. In engineering mechanics, several phenomena occurring in the material during deformation could be interpreted as damage: the appearance of microcracks and microvoids, but also, other phenomena that affect in an overall degradation of material properties.
As part of the research, two approaches for defining damage in the material are developed. In both cases, a scalar measure of isotropic damage governs the level of damage as the internal variable. The first approach uses the basic principles of continuum damage mechanics - effective stress concept and strain equivalence principle. The second approach is based on the analytical solution for the stress-strain relation until the complete failure. For the axially loaded members and truss structure, resulting forces are obtained exactly, since the stress is defined as analytical expression. On the other hand, for complex beam bending, determination of the resulting section forces is accomplished through the stress integration. The evaluated stress in one fiber element is determined by using either of two approaches for defining damage. Correspondingly, it is possible to model various type of material behavior (failure modes) of structural elements and the analysis of progressive damage evaluation in the cross section.